範例要從一個浪漫的故事說起……
一個男生開著車,在一個暴風雨的晚上。
經過一個車站,三人正焦急的等公車。一位是需要急救的老人;另外一位是醫生,他正在照顧那位老人;
最後一位則是他的夢中情人。但男生的車只能再坐一個人。
Liang Bo Wang, 2013-11-16
Liang Bo Wang、 線上版投影片 Under CC 3.0 BY TW License

pic source: http://seuconteudonaweb.wordpress.com/2013/08/06/a-big-analise-de-dados/

根據統計的資料顯示,床是全世界最危險的地方,因為大多數的人都是死在床上,所以如果你想活久一點,千萬別上床。
慶祝生日有利於延長壽命,因為統計表明,
那些活得越長的人,過的生日也越多。
統計是門不精確的科學。
R 滴!有統計背景會更懂,但今天不刻意提理論,歡迎結束後來討論。
善用 data.frame 相關的 filtering。
詳見
Subsetting, Advanced R programming by Hadley Wickham
iris # a built-in data.frame
iris[, c('Sepal.Length', 'Petal.Width')]
iris[iris$Species == 'setosa', ]
# 以下兩行結果相同
iris[iris$Sepal.Length > 7.5 & iris$Petal.Width < 2.2, ]
subset(iris, Sepal.Length > 7.5 & Petal.Width < 2.2)
大部份內建的函數可以處理 vector,不用自己寫迴圈,也較快。
> exp(1)
[1] 2.718282
> exp(c(1, 2, 4, 6))
[1] 2.718282 7.389056 54.598150 403.428793
> cos(c(0, pi))
[1] 1 -1
mean, var, sd, cor
min, max, median
abs, round
range # 回傳 c(min, max)
choose # C(n, x)
factorial # n!
# log 版
lchoose, lfactorial
quantile # Ex. 基測 PR 值
# 懶人包,針對物件多型結果不同
summary(1:10)
summary(factor(
c('a', rep('b', 3))
))
# 對 data.frame 也行
summary(iris)
# 連加、連除
> prod(1:4)
[1] 24
> sum(1:10)
[1] 55
> cumprod(1:4)
[1] 1 2 6 24
> cumsum(1:5)
[1] 1 3 6 10 15
> table(c(1:5, 1, 1, 3))
1 2 3 4 5
3 1 2 1 1
# misc.
is.na #判斷是否有 NA
seq #建一個數列
rep #重覆一段數列
diff #數列項目間的差
R 內建了許多分配函數。一般而言,一個分配會有以下 4 種 function,以常態分配 \(X \sim Norm(0, 1)\) 為例。
| Function | Description | Math Form |
d... |
Probability Density Fun. (PDF) | \(P(X \leq x) = \int_{-\infty}^x f_X(x) dx\) |
p... |
Cumulative Density Fun. (CDF) | \(P(X \leq x)= F_X(x)\) |
q... |
Quantile Fun. (inverse CDF) | \(q \to x\) s.t. \(F_X(x) = q\) |
r... |
Random Number Generator | generate \(\{X_i\}\) |
dnorm |
$$f_X(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$$ |
|
pnorm |
$$F_X(x) = \int_{-\infty}^{x}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} dx$$ |
|
qnorm |
$$F^{-1}_X(q) = x \\ q\in(0, 1)$$ |
|
rnorm |
$$X_1, \ldots, X_n \overset{iid}{\sim} Norm(0, 1)$$ |
|
一個男生開著車,在一個暴風雨的晚上。
經過一個車站,三人正焦急的等公車。一位是需要急救的老人;另外一位是醫生,他正在照顧那位老人;
最後一位則是他的夢中情人。但男生的車只能再坐一個人。
輕輕地交出手中的車鑰匙,交給醫生載老人去醫院。
陪自己的夢中情人等公車,浪漫就此開展……
我們知道公車來的時間是不固定的……一個隨機事件
$$T \sim Gamma(a, b)$$
Gamma 分配有以下特性: $$ E[T] = \frac{a}{b}, ~ Var[T] = \frac{E[T]}{b}$$
假設公車 15 分鐘來一班,則 $$a=15, b=1$$
bus.gamma <- function(t) dgamma(t, 15, 1)
curve(bus.gamma, from=0, to=50)
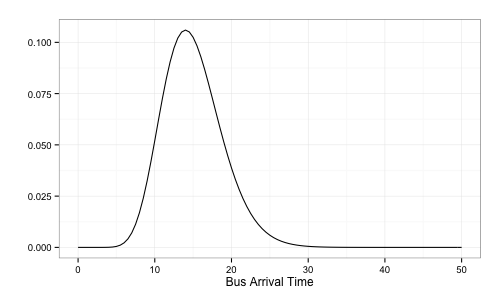
為何不用 \(a = 7.5, b = 0.5\) ?
公車超過 18 分鐘才來的機率? $$ P(T > 18) = 1 - P(T \leq 18) $$
1 - pgamma(18, 15, 1)
# 0.208 橘色區域
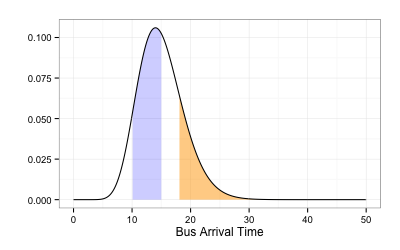
公車 10 - 15 分鐘來的機率? $$\begin{align} &P(10 < T \leq 15) \\ = &P(T \leq 15) - P(T \leq 10) \end{align}$$
pgamma(15, 15, 1) -
pgamma(10, 15, 1)
# 可以更簡潔寫成
diff(pgamma(c(10, 15), 15, 1))
# 0.451 藍色區域
| Dist. Name | PDF or PMF | 參數、說明 |
Uniform unif\(Unif(a, b)\) |
$$ f(x) = \frac{1}{b-a} $$ |
\(a\): |
Binomial binom\(Binomial(n, p)\) |
$$ P(x) = {n \choose x}\,p^x\,(1-p)^{n-x} $$ |
\(n\): |
Beta beta\(Beta(a, b)\) |
$$ f(x) = \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} x^{a-1} (1-x)^{b-1} $$ |
\(a\): |
Gamma gamma\(Gamma(\alpha, \beta)\) |
$$ f(x) = \frac{\beta^\alpha}{\Gamma(\alpha)} x^{\alpha-1}e^{-\beta x} $$ |
\(\alpha\): |
Poisson pois\(Poisson(\lambda)\) |
$$ P(x) = \frac{\lambda^x}{x!}e^{-\lambda} $$ |
\(\lambda\): |
Exponential exp\(Exp(\lambda)\) |
$$ f(x) = \lambda e^{-\lambda x} $$ |
\(\lambda\): |
Normal norm\(Norm(\mu, \sigma^2)\) |
$$ f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}} $$ |
\(\mu\): |
r... 都是。set.seed()
set.seed(633) # 接下來的亂數每次都會一樣
rnorm(1, 5, 10) # 17.36016
rexp(1, 1) # 1.130437
使用 sample() 函式
set.seed(633)
sample(1:10, size=5) # 9 1 3 5 2
# 取後可放回(樣本可重覆)
sample(1:10, size=5, replace=TRUE) # 10 5 3 10 6
# 不限數字
sample(c("m", "a", "9")) # "9" "a" "m"
也可以給 sample 權重
sample(
c("ma", "throw", "to", "slipper"),
prob=c(1, 2, 4, 8),
size=10, replace=TRUE
)
# [1] "slipper" "slipper" "to"
# [4] "slipper" "slipper" "slipper" "slipper"
# [8] "slipper" "ma" "to"
TRUE)
EXP_REP <- 5000 # 模擬次數
early_arrival_p <- function(girl_n, th) {
exp.sim <- replicate(
EXP_REP,
any(rgamma(girl_n, 15, 1) <= th)
)
mean(exp.sim) # return the rate having TRUE event
}
least.prob <- 0.8 # 超過 8 成機率
# 猜 N 從 1 到 30 附近
which.max(
sapply(1:30, function(n) early_arrival_p(n, 10)) > least.prob
) # return 19
$$\{T_i\}^N_{i=1} \overset{iid}{\sim} Gamma(15, 1)$$
$$\begin{align*} & P(T_{th} \text{ 分鐘有任一女生等到公車}) \\ &= 1 - P(T_{th} \text{ 分鐘沒有女生等到公車}) \\ &= 1 - P(T_1 > T_{th} \cap T_2 > T_{th} \cap \cdots \cap T_N > T_{th}) \\ &= 1 - \prod_{i=1}^N P(T_i > T_{th}) \\ &= 1 - \prod_{i=1}^N \left[ 1 - P(T_i \leq T_{th}) \right] > 0.8 \end{align*}$$
$$\prod_{i=1}^N \left[ 1 - P(T_i \leq T_{th}) \right] = p^N < 0.2$$ $$~ p = 1 - P(T_i \leq T_{th})$$
\(p\) 可由 1 - pgamma(th, 15, 1) 求得。
最後可以得到 \(N\) 的最小值。在此 \(N\geq19\)
$$
N > \frac{\log 0.2}{\log p}
$$
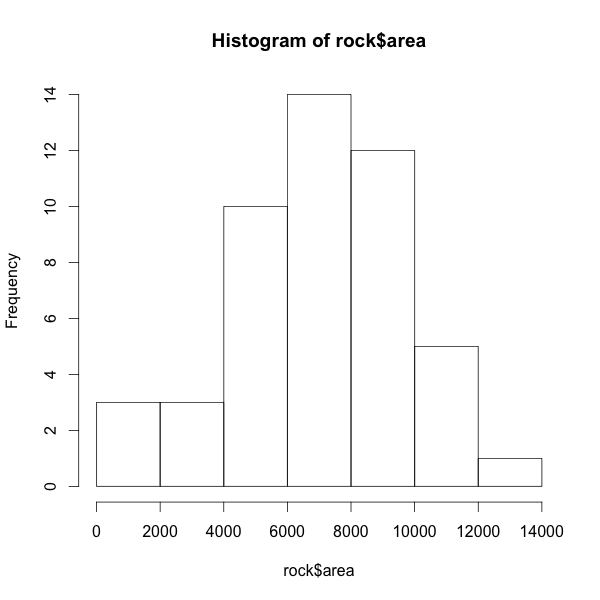
手邊沒有資料玩的話,data() 查詢內建的 datasets
以 rock 為例,
hist(rock$area)
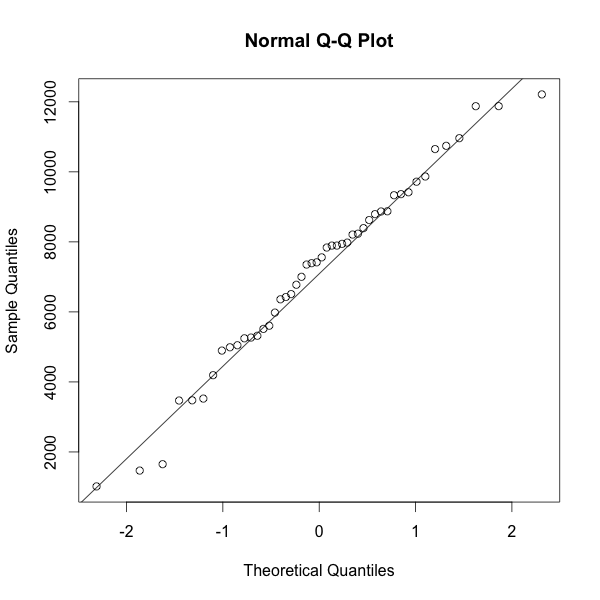
查看抽樣的分布
選擇常態分布,適不適合?
qqnorm(rock$area)
# or qqplot
qqline(rock$area)
我們學會了估計一個機率分布(點估計)。
如果今天是區分兩組資料的平均值是不是「不一樣」…
這組蠻好判斷的
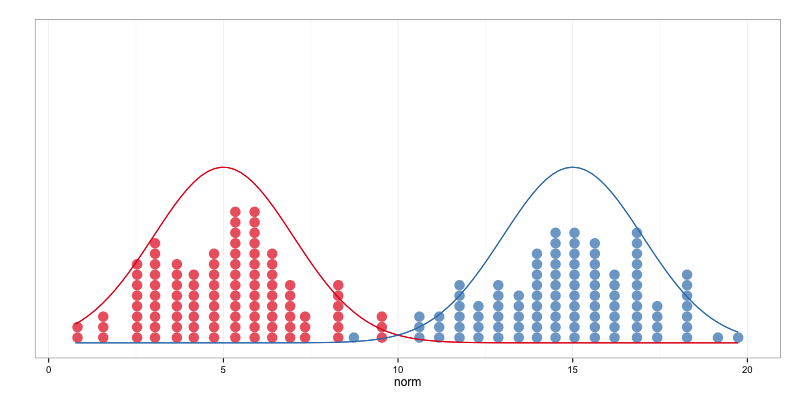
那這組呢?
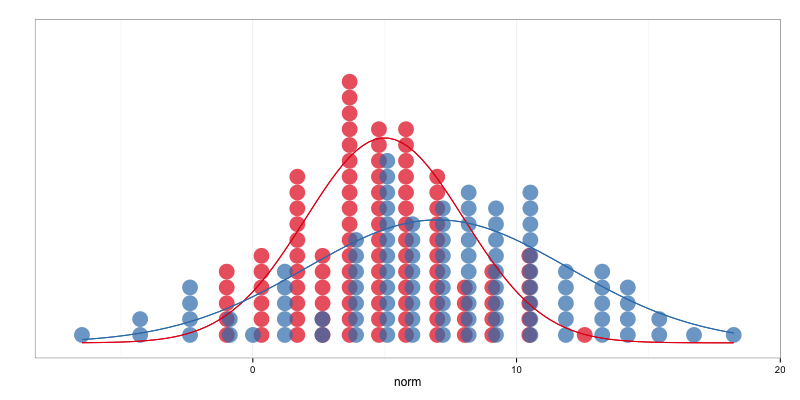
R 內建了大部份的檢定。
> model.iris <- lm(
Sepal.Length ~ Petal.Length + Petal.Width,
data=iris
)
# 建立模型不會有任何 output
> summary(model.iris)
# ... trimmed ...
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.19058 0.09705 43.181 < 2e-16 ***
Petal.Length 0.54178 0.06928 7.820 9.41e-13 ***
Petal.Width -0.31955 0.16045 -1.992 0.0483 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# ... trimmed ...
搜尋 Keyword
formulalmconfint