Convolutional Neural Network From the Ground Up

Far more details about DNN (CNN) are left out of this talk due to the time constraint. However, you should get the idea how to implement the core parts and be able to read the rest of the materials yourself.

About Me

• Master student at
  Bioinfo & Biostat Core Lab, NTU CGM
• R / Python
• Taiwan R co-organizer
• PyCon APAC 2014-15/TW staff
• Former intern at Microsoft Research Asia
• Happy to chat about Bioinfo and anime

CNN / DL are end-to-end classification

Ref: Deeplearning.net LeNet tutorial

• The CNN idea exists for 15+ years [LeCun 1998]
• A feeding frenzy in recent 5 fives thanks to tons of news coverage and GPU computation
• We will implement it with our bare hands today (though skipping a lot)

General machine learning framework

1. A mapping function \(f\) from input features \(x\) to scores of output class \(f\). Class with highest score is chosed as the prediction for input \(i\). $$ \begin{aligned} \hat{y_i} = \arg\max_j f(x_i; W)_j \\ j, y_i \in \{1 \ldots K\} \end{aligned} $$
2. A loss function \(L\) to compute the difference between \(y_i\) and \(\hat{y_i}\).
3. Optimize (Lower) the loss by updating the parameter \(W\).
4. Stop the update when max iterations are reached or stop criteria meets.

Linear classifier

Training dataset of images \(x_i \in R^D\) each with label \(y_i\) for \(N\) examples, \(i = 1 \ldots N\) and \(y_i \in 1 \ldots K\). $$f(x_i; W, b) = W x_i + b \quad\quad f: R^D \mapsto R^K$$ where parameters are \(W\) [K x D] called weights and \(b\) [K x 1] called bias vector.

In CIFAR-10 dataset, \(N\) = 50,000, \(D\) = 32 x 32 x 3 = 3072, \(K\) = 10.

Linear classifier visualized

Ref: CS231n Note: Linear Clasification

Bias trick

Ref: CS231n Note: Loss optimization

Loss function - Softmax

$$ L_i = -\log\left(\frac{e^{f_{y_i}}}{\sum_j e^{f_j}}\right) $$ \(e^{f_{y_i}}\) is like probability yet being normalized. Ex. \(-\log 10 < -\log 0.01 \). Higher score leads to lower loss.
For numerical stability, in computation \( \frac{e^{f_{y_i}}}{\sum_j e^{f_j}} = \frac{C \cdot e^{f_{y_i}}}{C \cdot \sum_j e^{f_j}} = \frac{e^{f_{y_i} + \log C}}{\sum_j e^{f_j + \log C}} \) and let \( \log C = -\max_j f_j \) to normalized the exp. of the largest score to be 1.

L2 Regularization

• Set of parameters \(W\) having the lowest loss is not unique. \(\phi W, \phi > 1\)
• Regularization of \(L2\) norm and a hyperparameter \(\lambda\) to tune the strength $$ R(W) = \sum_k\sum_l W_{k,l}^2 $$
• Full loss function includes avg. data loss and regularization loss $$ L = \underbrace{ \frac{1}{N} \sum_i L_i }_\text{data loss} + \underbrace{ \lambda R(W) }_\text{regularization loss} $$

Regularization (cont'd)

• Penalizing large weights tends to improve generalization.
• For example, $$ x = [1, 1, 1, 1] \quad w_1 = [1, 0, 0, 0] \quad w_2 = [0.5, 0.5, 0.5, 0.5]$$ where their L2 penalty are 0.5 and 0.25 respectively, \(w_2\) is preferred.
• L2 penalty prefers smaller and more diffuse weight vectors. Imply using more input dimensions instead of betting on one or two.

Loss optimization

• How to update the parameters based on this loss function?
• It's like being lost in a mountain and try to find a way home, no map.
• Height analogs to our loss function; position is our 2D parameters.
• Strategy: gradients of the loss function.
  Feel feet on your ground, follow the slope of hills. $$ \frac{df(x)}{dx} = \lim_{h\ \to 0} \frac{f(x + h) - f(x)}{h} $$
• Aka numerical gradients. Practically use \([f(x + h) - f(x - h)] / 2h\)

Choose the step size (learning rate)

Ref: CS231n Note: Linear Clasification

Analytical gradients

• Numerical gradients is slow (think of computing this for all \(W\) dimensions.
• We know Calculus ... so what's the gradient of softmax? $$ \frac{\partial L_i}{ \partial f_j} = - \left[\mathbb{1}(i = j) - p_j\right] \quad p_i = \frac{e^{f_i}}{\sum e^{f}} \quad \frac{\partial f_j}{ \partial w_j} = x_j $$
• Use the chain rule to get the gradient for \(\frac{\partial L_i}{ \partial w_j} = \frac{\partial L_i}{ \partial f_j} \cdot \frac{\partial f_j}{ \partial w_j}\)
• Already on edge? Check with the numerical gradients.

Gradient Descent

      # Vanilla Minibatch Gradient Descent
while it < max_iter:
    data_batch = sampling(data, 256)
    dw = gradient(loss_fun, data_batch, w)
    w += - step_size * w
      

Stochastic Gradient Descent (SGD) when batch contains only 1 sample.

Get our hands wet

For what does the CIFAR-10 dataset look like and data preprocessing, try ænotebook 00.

For softmax linear classifier, try notebook 01.

Our "artifact" neuron as a linear classifier

Ref: CS231n Note: Neural Network 1

We model the neuron by two parts: linear combination \(\sum w_i x_i\) and activation function \(f\)

Choices for activation function

• Traditionally, sigmoid \(\sigma(x) = 1 / (1 + e^{-x})\) and tanh.
• We use ReLU (The Rectified Linear Unit): $$f(x) = max(0, x)$$
• There remains many alternatives, such as leaky ReLU and maxout.
• Activation function introduces the non-linearity.

Fully-connected layer

Ref: CS231n Note: Neural Network 1

Total size of parameters (weights and biases) [input x #neuron]:
Left is (3 + 1) x 4 + (4 + 1) x 2 = 26.
Right is (3 + 1) x 4 + (4 + 1) x 4 + (4 + 1) x 1 = 41.

Example feed-forward computation

# forward-pass of a 3-layer neural network:
f = lambda x: np.where(x > 0, x, 0)  # ReLU activation
x = np.random.randn(3, 1)    # input vector (3x1)
h1 = f(np.dot(W1, x) + b1)   # 1st hidden layer (4x1)
h2 = f(np.dot(W2, h1) + b2)  # 2nd hidden layer (4x1)
out = np.dot(W3, h2) + b3    # output neuron (1x1)
      

The dim of Ws, bs: W1(4x3), b1(4x1), W2(4x4), b2(4x1), W3(4x1), b3(1x1)
Note that x can be (3xN) for batch input; no act. fun. in output layer.

Backward propagation

• Response of output layer, \(out\), goes to the loss function.
• Loss function returns the update direction for response, \(\Delta out\).
• But how to modify \(W\)s and \(b\)s to yield the desired change of \(\Delta out\)?
• Recall Calculus ... Use chain rule $$ \begin{aligned} f(x,y) = x y \quad &\rightarrow \quad \frac{\partial f}{\partial x} = y \quad \frac{\partial f}{\partial y} = x \\ f(x,y) = x + y \quad &\rightarrow \quad \frac{\partial f}{\partial x} = 1 \quad \frac{\partial f}{\partial y} = 1 \\ f(x,y) = \max(x, y) \quad &\rightarrow \quad \frac{\partial f}{\partial x} = \mathbb{1}(x >= y) \quad \frac{\partial f}{\partial y} = \mathbb{1}(y >= x) \end{aligned} $$

Backward propagation example

Think of a sigmoid function, \( f(w,x) = \frac{1}{1+e^{-(w_0x_0 + w_1x_1 + w_2)}} \).
First compute all the building blocks, $$ \begin{aligned} f(x) = \frac{1}{x} \quad &\rightarrow \quad \frac{df}{dx} = -1/x^2 \\ f_c(x) = c + x \quad &\rightarrow \quad \frac{df}{dx} = 1 \\ f(x) = e^x \quad &\rightarrow \quad \frac{df}{dx} = e^x = f(x) \\ f_a(x) = ax \quad &\rightarrow \quad \frac{df}{dx} = a \end{aligned} $$ Given initial w0, x0, w1, x1, w2 values (cont'd on next page)

Backward propagation example (cont'd)

Ref: CS231n Note: Optimization 2

Backprop in practice

• Compute all backprop gradients. Ex. Compute both dW and dx.
• Cache forward pass variables. Ex. Cache all W, x
• Since it is chain rule, always multiply the gradients from upper stage.
• Common gates (acts like): add (pass), max (switch) and multiply (swap).
• How to expand to matrix-matrix gradient computation?
• Dimension of x and dx match.

Matrix-Matrix multiply gradient

# forward pass
W = np.random.randn(5, 10)
X = np.random.randn(10, 3)
D = W.dot(X)  # shape (5, 3)
# ... suppose we had the gradient on D from upper stage
dD = np.random.randn(*D.shape)  # same shape as D
dW = dD.dot(X.T)  # X.T = X's transpose matrix
dX = W.T.dot(dD)

Get our hands wet

Now we are able to make a 2-layer fully connected (FC) NN, which has the structure: input - FC layer - ReLU - FC layer - softmax - out class

It's in notebook 02.

But I'm afraid we are almost running out of time so probably just see the final result to get the whole picture.

Before learning: sanity checks tips/tricks

• Gradient check using numerical gradients.
• Turn off regularization to check for correct loss at chance performance. Ex. CIFAR-10 initial softmax loss is around 2.302 (= -ln 0.1).
• Increase regularization should increase loss.
• Overfit a tiny subset of data (e.g. 20 samples).

Back on parameter updates

• Previously we use SGD and an analogue of finding path in mountains to home by approaching the inverse direction of slope.
• In real world, the slope controls the acceleration rate not the speed itself.
• Learning rate decay.
• Momentum update: \(mu \in [0, 1)\)

v = mu * v - learning_rate * dx # integrate velocity
x += v # integrate position
          

Parameter update method comparison

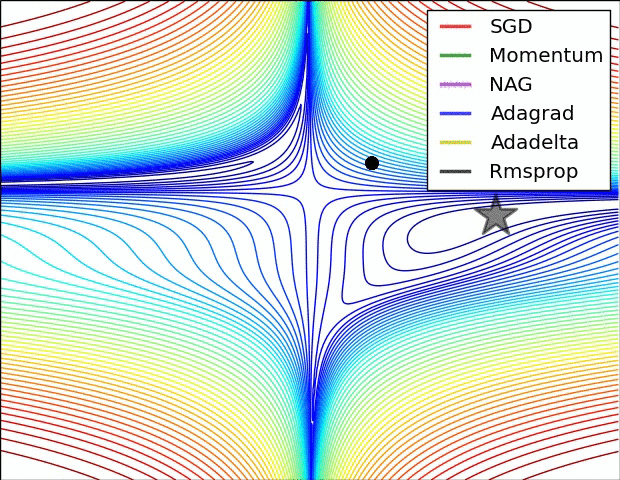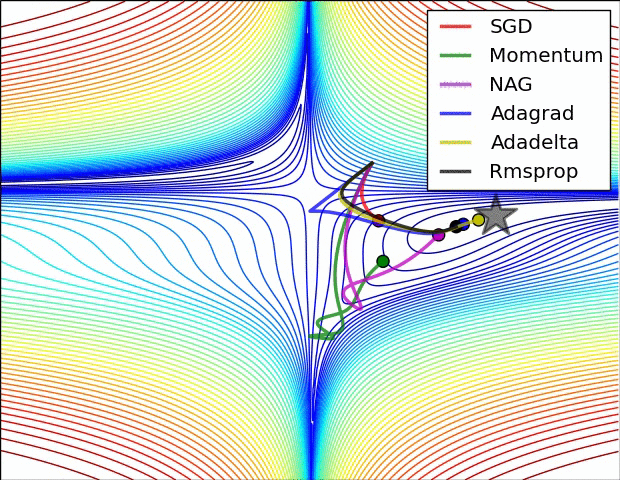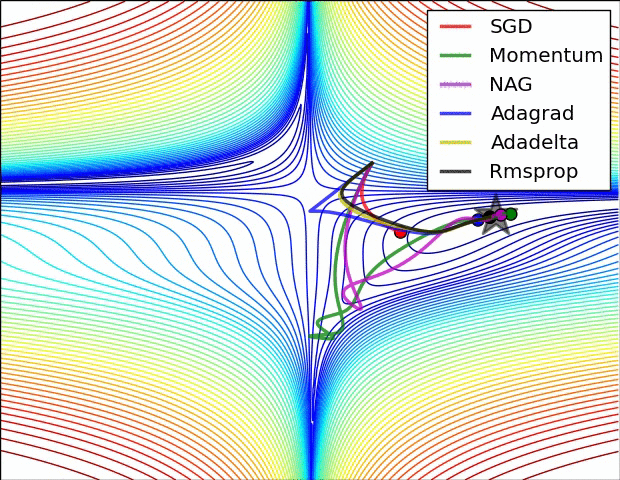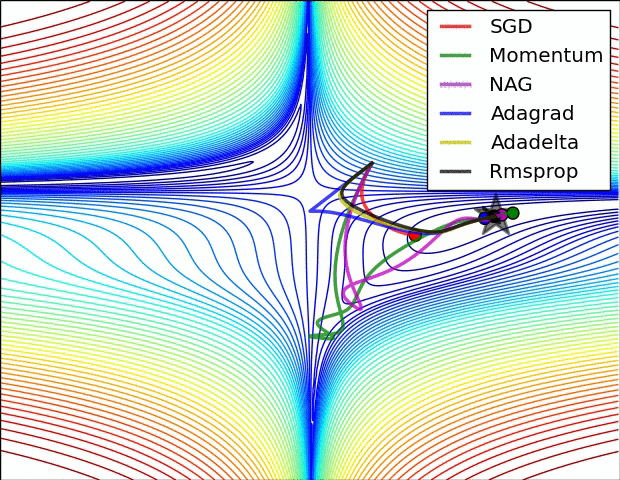
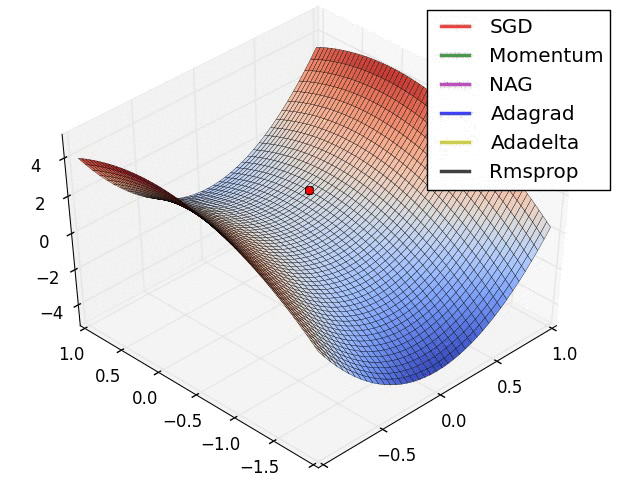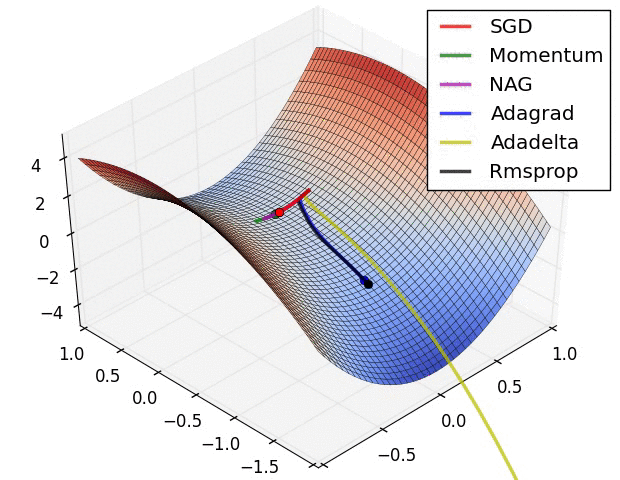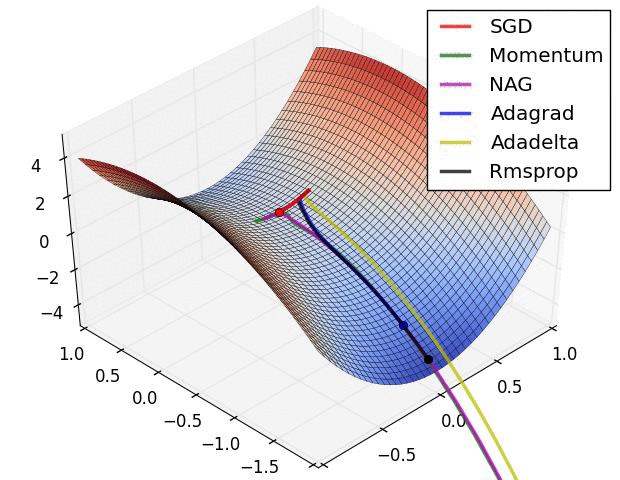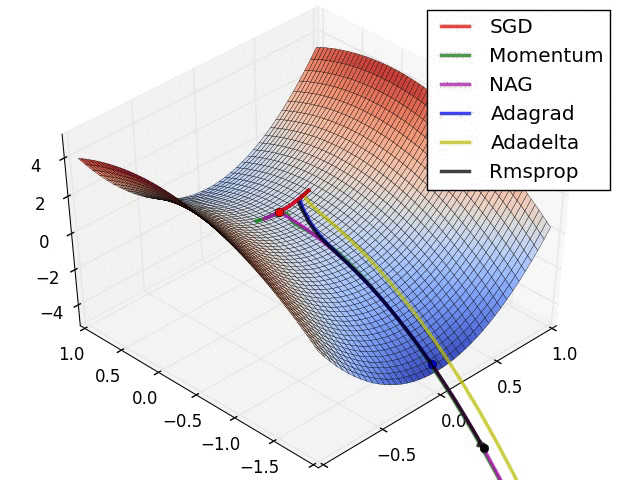
Animations that may help your intuitions about the learning process dynamics. Left: Contours of a loss surface and time evolution of different optimization algorithms. Notice the "overshooting" behavior of momentum-based methods, which make the optimization look like a ball rolling down the hill. Right: A visualization of a saddle point in the optimization landscape, where the curvature along different dimension has different signs (one dimension curves up and another down). Notice that SGD has a very hard time breaking symmetry and gets stuck on the top. Conversely, algorithms such as RMSprop will see very low gradients in the saddle direction. Tue to the denominator term in the RMSprop update, this will increase the effective learning rate along this direction, helping RMSProp proceed.

Ref: CS231n Note: Neural Network 3 and Image credit: Alec Radford.

ConvNet introduces depth

Ref: CS231n Note: Convolutional Netowrks

Input viewed as 32 width x 32 height x 3 channels (depth)
Output viewed as 1 x 1 x 10. Spatial information is preserved.

Ref: CS231n Note: Convolutional Netowrks

Receptive field: height and width of the spatially bounded input of all depths the neuron next stage takes from the former layer.

Convolutional layer - spatial arrangement

• Depth: multiple neurons receiving signals from the same receptive field forms a depth column
• Stride: overlapping between adjacent receptive fields
• Zero-padding: to maintain the W x H dimension of next layer, pad the input with zeros on the border of the input volume
• Given input volume size \(W\), receptive field size \(F\), stride size \(S\) and amount of zero padding \(P\), the output dimension is $$ (W-F + 2P) / S + 1 $$

Receptive field vs output size example

Ref: CS231n Note: Convolutional Netowrks

Conv. layer - spatial arrangement (cont'd)

• Use of zero padding: when \(P = (F - 1) / 2\) and \(S=1\), the input volume and output volume have same size.
• Not every stride value is feasible.
• Ex. 2012 ImageNet Krizhevsky et al. architecture uses input size [227x227x3], fist Conv layer uses F = 11, S = 4, P = 0 and depth K = 96.
  The output volume should be (227 - 11 + 2 x 0) / 4 + 1 = 55, [55x55x96]. Each neurons in the Conv layer has receptive field [11x11x3].

Conv. layer - parameter sharing

• Now we have 55x55x96 = 290,400 neurons in the first Conv layer, and each has 11x11x3 = 363 weights + 1 bias. Together this adds up to 290,400 x 364 = 105,706,600 parameters for the first layer alone.
• Assumption: neurons at same depth share same parameters
• So now parameters reduce to (363 + 1) x 96 = 34,944 parameters.
• Neurons at same depth use same parameters, referred as filter or kernel
• These 96 filters of first Conv layer can be visualized.

ImageNet 1st Conv layer filter visualization

Ref: CS231n Note: Convolutional Netowrks

Conv. layer - summary

• Accepts a volume of size \(W_1 \times H_1 \times D_1 \)
• Four hyperparameter: depth(#filters) \(K\), receptive field size \(F\), stride \(S\) and amount of zero padding \(P\)
• Produces a volume of size \(W_2 \times H_2 \times D_2\), where \(W_2 = (W_1 - F + 2P)/S + 1\), and \(D_2 = K\)
• With parameter sharing, it introduces \(F \cdot F \cdot D_1\) weights per filter, thus for a total of \((F \cdot F \cdot D_1) \cdot K\) weights and \(K\) biases.

Max Pooling Layer

Ref: CS231n Note: Convolutional Netowrks

Converting FC layer to CONV layers

An FC layer with \(K = 4096\) looking at Conv layer of [7x7x512] volumes, using filter size \(F = 7\) gives output volume [1x1x4096].

An FC layer looks at the previous layer with \(K = 1000\) and \(F=1\) gives output [1x1x1000].

That's all you need for a ConvNet :)

Layer Patterns

INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC

• INPUT -> CONV -> RELU -> FC
• INPUT -> [CONV -> RELU -> POOL]*2 -> FC -> RELU -> FC
• INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL]*3 -> [FC -> RELU]*2 -> FC
• Multiple stacked CONV layers can develop more complex features of the input volume before the destructive pooling operation

You should be able to read these CNNs

Ref: Deeplearning.net LeNet tutorial

Ref: EBLearn LeNet-5

Get our hands wet

Notebook 03 works forward/backward implementation for all types of layer.

Notebook 04 creates a CONV-RELU-POOL-FC two-layer ConvNet.